Σε έναν κόσμο χωρίς κρυπτογράφηση δεδομένων, θα ήταν αδύνατον να έχουμε ένα προσωπικό email, έναν προσωπικό λογαριασμό στο facebook, ή να χρησιμοποιήσουμε μια πιστωτική κάρτα για αγορές στο Internet. Η κρυπτογράφηση δεδομένων χρησιμοποιείται παντού, και είναι η “κλειδαριά” που κρατάει την ψηφιακή μας ζωή ασφαλή. Ας δούμε πώς λειτουργεί.
Προτάσεις συνεργασίας
Τα νέα άρθρα του PCsteps
Γίνε VIP μέλος στο PCSteps
Ανανεώσαμε αυτόν τον οδηγό επ' ευκαιρία της πρόσφατης ανακάλυψης του μεγαλύτερου πρώτου αριθμού μέχρι στιγμής, με μήκος 22 εκατομμυρίων ψηφίων, καθώς οι πρώτοι αριθμοί είναι ζωτικής σημασίας για την κρυπτογράφηση δεδομένων.
Η θεωρία και η πράξη
Ο οδηγός αυτός αναφέρεται στη θεωρία της κρυπτογράφησης και πως εφαρμόζεται στο Internet.
Αν ενδιαφέρεστε για κρυπτογράφηση δεδομένων στον υπολογιστή σας, δείτε τον οδηγό μας:
Κρυπτογράφηση Αρχείων Με το VeraCrypt.
Τι είναι η κρυπτογράφηση δεδομένων
Η φράση “κρυπτογράφηση δεδομένων” ακούγεται μυστηριώδης και εξωτική.
Και μόνο στην αναφορά της φανταζόμαστε ιδιοφυείς χάκερ να χειρίζονται υπερυπολογιστές σε εργαστήρια κρυμμένα στα έγκατα της γης, σε συνθήκες απόλυτης μυστικότητας, με στρατιωτική φρουρά.

Στην πραγματικότητα, όμως, η βασική λογική πίσω από την κρυπτογράφηση δεδομένων είναι εξαιρετικά απλή.
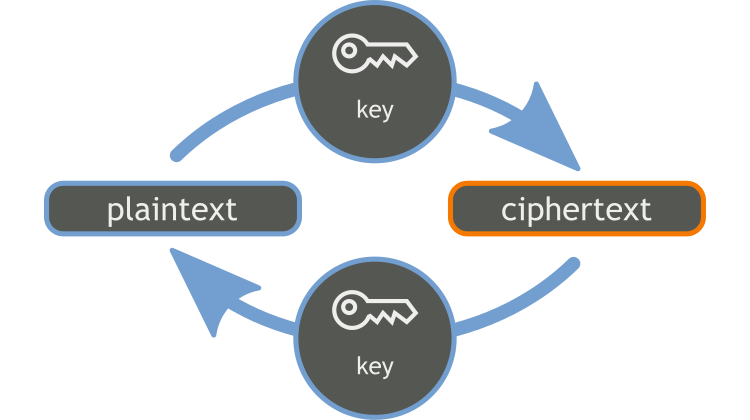
Αφορά το πώς να “μεταμφιέσουμε” μια πληροφορία (ένα κείμενο, έναν αριθμό, ένα αρχείο), έτσι ώστε να μην βγάζει κανένα απολύτως νόημα στα μάτια τρίτων.
Μόνο όποιος έχει το “κλειδί” της κρυπτογράφησης θα μπορεί να διαβάσει την αρχική πληροφορία.

Ας δούμε για παράδειγμα τη φράση:
Αυτή τη στιγμή διαβάζετε PCsteps
Μια απλοϊκή μέθοδος για κρυπτογράφηση δεδομένων είναι να πάρουμε κάθε γράμμα της φράσης και το αντικαταστήσουμε με το γράμμα που βρίσκεται δεξιά του στο πληκτρολόγιο.

Η φράση που προκύπτει είναι:
σθυξ υξ δυοη,ξ φοσνσχρυρ [vdyr[d

Ο κανόνας για τη “μεταμφίεση” των δεδομένων ονομάζεται αλγόριθμος κρυπτογράφησης.
Η διαδικασία εφαρμογής του αλγόριθμου στα αρχικά δεδομένα ονομάζεται κρυπτογράφηση.
Η γνώση του πώς εφαρμόζεται αυτός ο κανόνας είναι το κλειδί της κρυπτογράφησης.
Η αντίστροφη διαδικασία εφαρμογής του αλγόριθμου στα κρυπτογραφημένα δεδομένα, ώστε να πάρουμε ξανά τα αρχικά δεδομένα, ονομάζεται αποκρυπτογράφηση.
Κρυπτογράφηση δεδομένων: Μια “πρόσφατη” επινόηση
Σύμφωνα με τον ιστορικό Πλούταρχο, οι Σπαρτιάτες στρατηγοί που ήθελαν να στείλουν μυστικά κάποιο μήνυμα ο ένας στον άλλο, τύλιγαν μια μακριά και λεπτή λωρίδα παπύρου σε ένα κυλινδρικό κομμάτι ξύλου, τη “σκυτάλη”, και έγραφαν εκεί το μήνυμά τους.

Ξετυλίγοντας τον πάπυρο, το κείμενο δεν έβγαζε κανένα νόημα, και μπορούσε να μεταφερθεί με ασφάλεια.
Στον προορισμό του, ο παραλήπτης θα τύλιγε το μήνυμα σε μια σκυτάλη του ίδιου μεγέθους για να το διαβάσει.
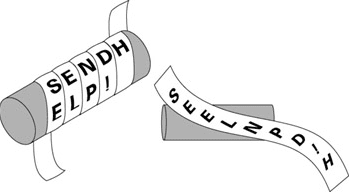
Στην προκειμένη περίπτωση:
- Ο αλγόριθμος κρυπτογράφησης είναι η χρήση του παπύρου και της σκυτάλης.
- Το ξετύλιγμα του παπύρου είναι η κρυπτογράφηση δεδομένων.
- Το κλειδί της κρυπτογράφησης είναι το ακριβές μέγεθος που πρέπει να έχει η σκυτάλη για να λειτουργήσει η αποκρυπτογράφηση – δηλαδή το τύλιγμα του γραμμένου παπύρου.
Ένα άλλο γνωστό είδος αλγορίθμου του αρχαίου κόσμου είναι το Caesar cipher ή Caesar shift.
Σε αυτόν, η κρυπτογράφηση δεδομένων γίνεται με λογική μετακίνηση του αλφάβητου ώστε κάθε γράμμα να αντιστοιχείται με το αντίστοιχο γράμμα τρεις θέσεις μπροστά ή πίσω.
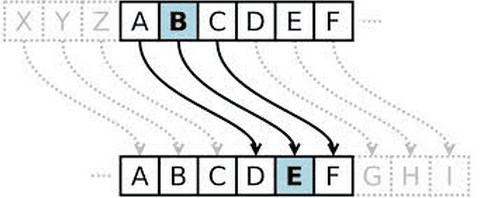
Το όνομα του αλγορίθμου προέρχεται από τον Ιούλιο Καίσαρα, που χρησιμοποιούσε αυτή τη μέθοδο σύμφωνα με τον ιστορικό Σουητώνιο.
Το πόσες θέσεις είναι η μετακίνηση (2, 3 ή περισσότερες) είναι το κλειδί της κρυπτογράφησης στο συγκεκριμένο αλγόριθμο.
Κατασκευές και συσκευές για κρυπτογράφηση δεδομένων
Στην πορεία τις ιστορίας επινοήθηκαν πολλοί ακόμα αλγόριθμοι για την κρυπτογράφηση δεδομένων, κυρίως από κράτη και κυβερνήσεις σε καιρό πολέμου.
Συχνά, για πιο περίπλοκους αλγορίθμους, που παρείχαν μεγαλύτερη ασφάλεια, χρησιμοποιούσαν ειδικές κατασκευές.

Οι κατασκευές αυτές αργότερα έδωσαν τη θέση τους σε ειδικές ηλεκτρομηχανικές συσκευές.
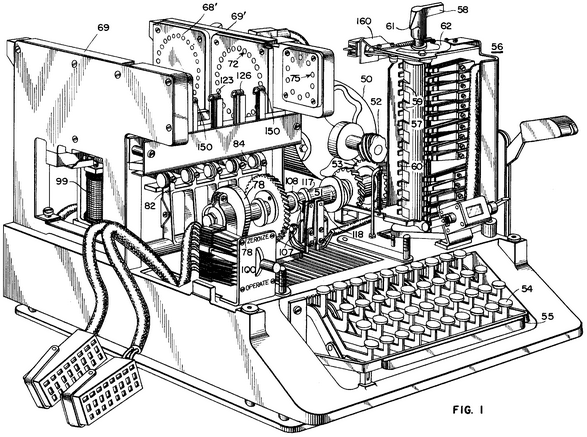
Μία από τις πλέον γνωστές συσκευές του είδους είναι η Enigma machine, την οποία χρησιμοποιούσε η Ναζιστική Γερμανία για την κρυπτογράφηση δεδομένων κατά τη διάρκεια του Β' Παγκοσμίου Πολέμου.

Η συσκευή χρησιμοποιήθηκε εκτεταμένα από την Γερμανική υπηρεσία πληροφοριών Abwehr, για την κρυπτογράφηση των πληροφοριών σχετικά με αεροπορικούς βομβαρδισμούς, την κίνηση στρατιωτικών μονάδων, και την τοποθεσία και το φορτίο στρατιωτικών πλοίων.
Μία άλλη σημαντική χρήση της Enigma ήταν η κρυπτογράφηση δεδομένων σχετικά με τη θέση των γερμανικών υποβρυχίων στον Ατλαντικό, τις εντολές που λάμβαναν, ίσως και το αν έγερναν.

Τα υποβρύχια αυτά είχαν αποκλείσει από θαλάσσης τη Βρετανία, θέτοντάς την πρακτικά σε κατάσταση πολιορκίας.
Το γεγονός πως ο Βρετανός μαθηματικός και επιστήμονας των υπολογιστών Alan Turing κατάφερε να ανακαλύψει το κλειδί κρυπτογράφησης του Enigma (να “σπάσει” την κρυπτογράφηση) υπήρξε καθοριστικής σημασίας για την έκβαση του πολέμου.

(ασχέτως αν το 1952 καταδίκασαν τον Alan Turing καθώς ήταν ομοφυλόφιλος – που ήταν παράνομο τότε – και τον οδήγησαν στην αυτοκτονία… Τουλάχιστον η Βρετανική κυβέρνηση ζήτησε επισήμως συγνώμη… το 2009)
Η κρυπτογράφηση δεδομένων στους υπολογιστές
Σήμερα, κάθε κρυπτογράφηση δεδομένων βασίζεται σε υπολογιστές.
Πολύ απλά, όποιον αλγόριθμο κι αν επινοήσει ο άνθρωπος, όσο περίπλοκος κι αν είναι, είναι υπερβολικά εύκολο να τον σπάσει ένας κατάλληλα προγραμματισμένος υπολογιστής.

Η κρυπτογράφηση δεδομένων μέσω υπολογιστή γενικά ανήκει σε δύο κατηγορίες:
- Symmetric key encryption
- Public key ή Asymmetric key encryption
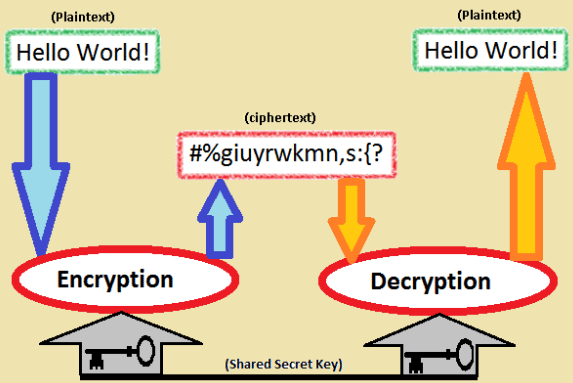
Symmetric key encryption
Στην κρυπτογράφηση symmetric key, όπως και οι Σπαρτιάτες στρατηγοί, και οι δύο υπολογιστές που επικοινωνούν χρειάζεται να έχουν το ίδιο κλειδί κρυπτογράφησης.
Στην περίπτωση των υπολογιστών το κλειδί είναι ένας αριθμητικός κωδικός, το μέγεθος του οποίου ορίζεται από το πόσα bits τον αποτελούν.
(Για την εξήγηση των bits δείτε τον οδηγό μας: Πώς Λειτουργεί ο Υπολογιστής, Απλά και Κατανοητά)
Ο πρώτος σημαντικός αλγόριθμος για κρυπτογράφηση δεδομένων μέσω υπολογιστή ήταν ο Data Encryption Stantard (DES) που αναπτύχθηκε από την IBM στις ΗΠΑ και εγκρίθηκε για χρήση το 1970.
Ο DES χρησιμοποιεί κλειδί μήκους 56-bit, που διαθέτει πάνω από 72 τετράκις εκατομμύρια πιθανούς συνδυασμούς (72.057.594.037.927.936, για την ακρίβεια).
Μπορεί να ακούγονται ατέλειωτοι, όμως το 1998 δημιουργήθηκε η συσκευή EFF DES cracker (“Deep Crack”), με ειδικά κατασκευασμένα τσιπάκια, που επέτρεπαν σε έναν υπολογιστή να δοκιμάσει 90 δισεκατομμύρια κλειδιά το δευτερόλεπτο.

Θεωρητικά, θα χρειάζονταν 9 ημέρες για να δοκιμάσει κάθε πιθανό συνδυασμό.
Στην πράξη, ο Deep Crack κατάφερε να σπάσει τον DES σε δύο ξεχωριστά τεστ, στο πρώτο σε 56 ώρες και στο δεύτερο σε 22 ώρες, αποδεικνύοντας πως ο συγκεκριμένος αλγόριθμος είναι ανεπαρκής για την κρυπτογράφηση δεδομένων σε πραγματικές συνθήκες.

Πλέον, ο DES έχει αντικατασταθεί από τον αλγόριθμο Advanced Encryption Standard (AES), που χρησιμοποιεί κλειδιά 128, 192 ή 256-bit.
Με την αύξηση των bit, οι πιθανοί συνδυασμοί ανεβαίνουν εκθετικά. Ένα κλειδί 128-bit μπορεί να έχει πάνω από 300.000.000.000.000.000.000.000.000.000.000.000 πιθανούς συνδυασμούς.
Ο μεγαλύτερος υπερυπολογιστής αυτή τη στιγμή στον κόσμο, που μπορεί να εκτελέσει 33,86 petaflop/s (τετράκις εκατομμύρια υπολογισμούς το δευτερόλεπτο) και θα μπορούσε θεωρητικά να σπάσει τον DES σε 2 δευτερόλεπτα, θα χρειαζόταν περίπου 250 δισεκατομμύρια χρόνια για να ελέγξει όλους τους συνδυασμούς του AES-128.

Γνωστοί Αλγόριθμοι Symmetric key encryption
Εκτός από τον AES που προαναφέραμε, άλλοι γνωστοί αλγόριθμοι Symmetric key που χρησιμοποιούνται ευρέως για την κρυπτογράφηση δεδομένων είναι οι RC4, 3DES, IDEA, CAST5, Twofish, Serpent, Blowfish.
Public/asymmetric key encryption
Υπάρχει ένα σημαντικό πρόβλημα με την κρυπτογράφηση δεδομένων μέσω της μεθόδου symmetric key, ανεξαρτήτως αλγόριθμου, ειδικά όσον αφορά τη χρήση της στο Internet.
Το πρόβλημα είναι πως αν κάποιος θέλει να μας στείλει κάτι κρυπτογραφημένο με αυτή τη μέθοδο, για να το ανοίξουμε πρέπει με κάποιο τρόπο να μας στείλει και ένα αντίγραφο του κλειδιού.
Αν όμως μας στείλει το κλειδί μέσω του Internet, που είναι ένα δημόσιο δίκτυο, θα μπορούσε οποιοσδήποτε να το υποκλέψει κατά την αποστολή, και να έχει πρόσβαση στα κρυπτογραφημένα δεδομένα.

Αυτό το πρόβλημα λύνει η μέθοδος Public/asymmetric key encryption.
Ουσιαστικά, σε αυτή τη μέθοδο κρυπτογράφησης υπάρχουν δύο κλειδιά:
- Το Public key, είναι δημόσιο και μπορεί να το χρησιμοποιήσει οποιοσδήποτε για την κρυπτογράφηση δεδομένων.
- Το Private Key που είναι μυστικό. Συνδέεται μαθηματικά με το Public key και είναι απαραίτητο για την αποκρυπτογράφηση.
Για να γίνει κατανοητός ο τρόπος λειτουργίας αυτής της μεθόδου, θα χρησιμοποιήσουμε ένα παράδειγμα με δύο χρήστες, την Alice και τον Bob.

Tα ονόματα Alice και Bob, παρεμπιπτόντως, είναι τα στάνταρ ονόματα που χρησιμοποιούν οι κρυπτογράφοι για παραδείγματα και να δείξουν πώς λειτουργούν οι αλγόριθμοι.
Το πρόβλημα με την κρυπτογράφηση δεδομένων με symmetric key
Έστω λοιπόν πως η Alice θέλει να στείλει ένα μυστικό μήνυμα στον Bob μέσω του δημόσιου ταχυδρομείου, και περιμένει μια επίσης μυστική απάντηση από τον Bob.

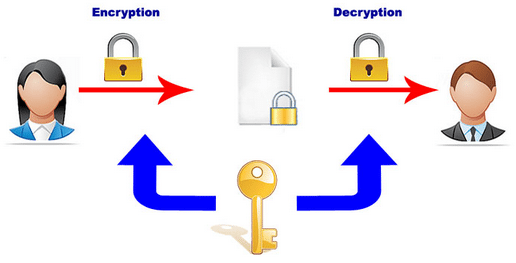
Στην κρυπτογράφηση δεδομένων με symmetric key, ουσιαστικά η Alice κλειδώνει το μήνυμα σε ένα κουτί, με ένα λουκέτο (αλγόριθμος κρυπτογράφησης) για το οποίο έχει μόνο εκείνη το κλειδί (κλειδί κρυπτογράφησης).
Ύστερα, στέλνει το κλειδωμένο κουτί με το ταχυδρομείο στον Bob. Και, αναγκαστικά, του στέλνει σε ένα ξεχωριστό φάκελο, μέσω ταχυδρομείου, ένα αντίγραφο του μοναδικού κλειδιού.

Κάποιος κακόβουλος, όμως, με πρόσβαση στο ταχυδρομείο, θα μπορούσε να αντιγράψει το κλειδί και να έχει μετά απεριόριστη πρόσβαση στην επικοινωνία της Alice και του Bob.

Η λύση της κρυπτογράφησης public/asymmetric key
Στην κρυπτογράφηση δεδομένων με Public/Asymmetric key, η Alice και ο Bob έχουν ξεχωριστά λουκέτα και ξεχωριστά κλειδιά.

Ο Bob στέλνει το λουκέτο του ανοιχτό (Public key) με το ταχυδρομείο στην Alice, αλλά κρατάει εκείνος το κλειδί (Private key).
Η Alice χρησιμοποιεί αυτό το λουκέτο για να κλειδώσει το κουτί με το μήνυμα, και στέλνει το κλειδωμένο κουτί στον Bob, που το ανοίγει με το κλειδί του.

Αντίστοιχα, αν θέλει ο Bob να στείλει μήνυμα, θα πρέπει να του στείλει η Alice το δικό της λουκέτο πρώτα.
Αυτή η μέθοδος έχει το τεράστιο πλεονέκτημα πως δεν χρειάζεται να ανταλλάξουν κλειδιά ο Bob και η Alice, ώστε να μην υπάρχει η πιθανότητα να γίνει υποκλοπή κατά την ανταλλαγή.
Όμως, στην κρυπτογράφηση symmetric key, χρειάζεται μία μόνο φορά να σταλεί το κλειδί κρυπτογράφησης.

Στην κρυπτογράφηση δεδομένων με public/asymmetric key, χρειάζεται συνεχής ανταλλαγή δεδομένων σχετικών με την κρυπτογράφηση, εις βάρος της ταχύτητας μεταφοράς των πραγματικών δεδομένων. Συν ότι οι αλγόριθμοι αυτού του τύπου χρειάζονται περισσότερους υπολογισμούς.

Για να συνδυαστεί η ασφάλεια με την ταχύτητα, υλοποιείται μια υβριδική λύση για την κρυπτογράφηση δεδομένων, η οποία ουσιαστικά χρησιμοποιεί ταυτόχρονα και ένα αλγόριθμο symmetric key και έναν αλγόριθμο public/assymetric key.
Η υβριδική λύση που συνδυάζει ταχύτητα και ασφάλεια
Αυτή είναι η μέθοδος που χρησιμοποιείται ευρέως για την κρυπτογράφηση δεδομένων στο Internet.
Στην υβριδική αυτή λύση, για να στείλει η Alice μήνυμα στον Bob, ακολουθούνται τα εξής βήματα:
- Ο Bob στέλνει στην Alice το ανοιχτό του λουκέτο (Public Key), ενώ κρατάει το δικό του κλειδί (Private Key).
- H Alice αγοράζει ένα νέο λουκέτο με νέο, μοναδικό κλειδί (δημιουργία Symmetric key). Κλειδώνει με αυτό το κουτί με τα δεδομένα (data encapsulation).
- Σε ένα δεύτερο, ξεχωριστό κουτί, πολύ μικρότερου μεγέθους, βάζει ένα αντίγραφο του μοναδικού κλειδιού, και το κλειδώνει με το λουκέτο του Bob (key encapsulation).
- Στέλνει και τα δύο κουτιά στον Bob με το ταχυδρομείο.

Ο Bob, με τη σειρά του, μόλις λάβει και τα δύο κουτιά, ξεκλειδώνει με το κλειδί του το μικρό κουτί για να πάρει το μοναδικό κλειδί, και με το μοναδικό κλειδί ξεκλειδώνει το κουτί με τα δεδομένα.
Πλέον, εφόσον και ο Bob και η Alice έχουν ένα αντίγραφο του μοναδικού κλειδιού, που μεταφέρθηκε με ασφάλεια, όλη η υπόλοιπη επικοινωνία τους μπορεί να γίνει χωρίς την αποστολή κανενός κλειδιού.

Αυτή είναι μια σχετικά απλή έκδοση όσον αφορά την κρυπτογράφηση δεδομένων με Public/Asymmetric key.
Στην πράξη, στους πιο γνωστούς αλγόριθμους η Alice και ο Bob έχουν ο καθένας δύο κλειδιά, ένα για την κρυπτογράφηση δεδομένων και ένα για την αποκρυπτογράφηση.
Σε αυτή την αναλογία, η Alice μπορεί να εκδώσει οδηγίες για το πώς να φτιάξει κάποιος ένα λουκέτο (public key), όμως το συγκεκριμένο λουκέτο είναι σχεδιασμένο έτσι ώστε να είναι αδύνατον να εξαχθεί από αυτό συμπέρασμα για τη δημιουργία κλειδιού (private key).

Σε άλλα συστήματα με κρυπτογράφηση δεδομένων Public/Asymmetric key, η Alice και ο Bob επιλέγουν ένα τυχαίο κλειδί, και μετά επικοινωνούν για να συγκρίνουν τα χαρακτηριστικά των κλειδιών τους. Γνωρίζοντας τις διαφορές, δημιουργούν ένα κουτί με ειδική κλειδαριά, που ανοίγει μόνο με τα δικά τους κλειδιά.
Γνωστοί Αλγόριθμοι Public/Asymmetric key encryption
Ο ποιο γνωστός αλγόριθμος Public/Asymmetric key όσον αφορά το Internet είναι ο RSA, την ακριβή λειτουργία του οποίου θα αναλύσουμε παρακάτω..
Από εκεί και πέρα, γνωστές και διαδεδομένες τεχνικές public/asymmetric key για διάφορες εφαρμογές είναι το πρωτόκολλο ανταλλαγής κλειδιών Diffie-Hellman, το Digital Signature Standard που περιλαμβάνει τον Digital Signature Algorithm, η κρυπτογράφηση ElGamal, το σύστημα Paillier, το σύστημα Cramer-Shoup και το πρωτόκολλο YAK.
Πως υλοποιείται η κρυπτογράφηση δεδομένων στο Internet
Το κύριο πρωτόκολλο κρυπτογράφησης του Internet είναι το Transport Layer Security (TLS), που είναι ο διάδοχος του Secure Socket Layer (SSL). Είναι το πρωτόκολλο που ακολουθείται όποτε μπαίνουμε σε μια σελίδα που ξεκινάει με https:// και με λουκέτο.
Να σημειωθεί πως το TLS δεν είναι το ίδιο ένας αλγόριθμος κρυπτογράφησης. Είναι το πρωτόκολλο που υπαγορεύει τα βήματα που πρέπει να ακολουθηθούν για να πραγματοποιηθεί μια ασφαλής σύνδεση.
Τα βήματα αυτά συμπεριλαμβάνουν, μεταξύ άλλων:
- ποια στοιχεία χρειάζεται να ανταλλάξουν ο υπολογιστής μας και ο server πριν δημιουργηθεί η ασφαλής σύνδεση
- ποιος αλγόριθμος Public/Asymmetric key θα χρησιμοποιηθεί και για την κρυπτογράφηση ποιών δεδομένων.
- ποιος αλγόριθμος θα χρησιμοποιηθεί για το Symmetric key
- Πόσο διάστημα θα διαρκέσει η σύνδεση (session) πριν χρειαστεί να ανανεωθεί

Επίσης, ο TSL ορίζει και ένα επιπλέον μέτρο ασφαλείας, που ονομάζεται Digital Certificate.
Digital Certificate
Υπάρχουν κάποιες εταιρείες που ονομάζονται Certificate Authorities, όπως πχ η VeriSign, η DigiCert, το Comodo Group, και άλλες.

Οι εταιρείες αυτές εκδίδουν ένα ψηφιακό πιστοποιητικό (Digital Certificate). Ουσιαστικά πρόκειται για ένα μοναδικό κομμάτι κώδικα που επιβεβαιώνει πως ένα συγκεκριμένο Public key ανήκει σε μια συγκεκριμένη ιστοσελίδα και μια συγκεκριμένη επιχείρηση.
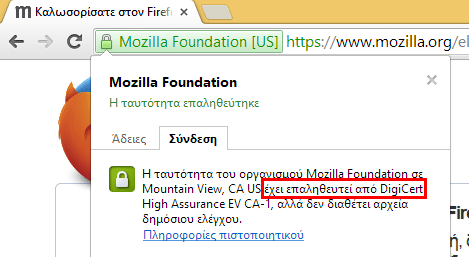
Έτσι, είναι αδύνατον κάποιος να πλαστογραφήσει πχ το Public key του Facebook. Εφόσον υπάρχει το https:// και το λουκέτο, βρισκόμαστε στο πραγματικό facebook…
…και όχι κάποια ψεύτικη σελίδα που παριστάνει πως είναι το Facebook για να κλέψει τον κωδικό μας.
Αν μπούμε σε κάποια ιστοσελίδα με https:// αλλά χωρίς Digital Certificate από κάποια Certificate Authority, ο browser θα μας προειδοποιήσει.
Η κρυπτογράφηση δεδομένων στο Internet, στην πράξη
Για να δούμε απλοποιημένα πως λειτουργεί το πρωτόκολλο TLS, μόλις μπαίνουμε σε μια σελίδα https://, γίνονται τα εξής:
- Ο browser στέλνει τα στοιχεία του στο server: ποιες εκδόσεις SSL και TLS υποστηρίζει, ποιους αλγόριθμους για την κρυπτογράφηση δεδομένων, στοιχεία που αφορούν το session (πχ ημερομηνία και ώρα έναρξης) και γενικά όσα στοιχεία χρειάζεται για να γίνει η σύνδεση.
- Ο web server της σελίδας στέλνει τα αντίστοιχα στοιχεία του όσον αφορά το SSL/TLS, τους αλγόριθμους, το session κλπ. Επίσης στέλνει το digital certificate.
- Ο browser ελέγχει τρία πράγματα:
- Αν το digital certificate προέρχεται από μια πιστοποιημένη Certificate Authority,
- Αν ισχύει ακόμα
- Αν συνδέεται με το site που έχουμε μπει.
- Εφόσον όλα είναι καλά, o server στέλνει το public key στον browser. Ο browser χρησιμοποιεί το public key για να δημιουργήσει ένα τυχαίο symmetric key.
- Το symmetric key αποστέλλεται στο server, και χρησιμοποιείται για όλη τη διάρκεια της σύνδεσης (session) σε κρυπτογράφηση δεδομένων τύπου symmetric key.
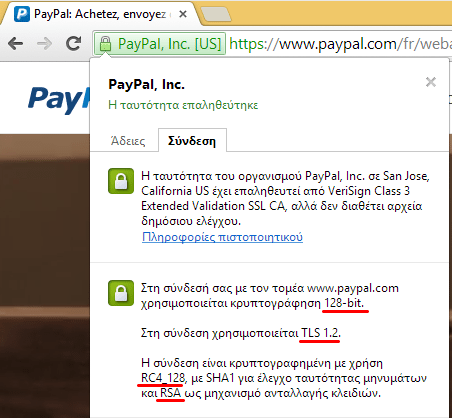
Μόλις αποσυνδεθούμε (πχ κάνουμε log-out από το email ή από το facebook ή λήξει το session, πχ στο paypal ή το ebanking), ο υπολογιστής μας και ο web server καταστρέφουν το symmetric key.
Στην επόμενη σύνδεση, θα δημιουργηθεί ένα εντελώς νέο symmetric key.
Ο πιο συνηθισμένος αλγόριθμος κρυπτογράφησης Public/asymmetric key που χρησιμοποιείται με το TLS είναι ο RSA.
Για να μάθουμε περισσότερα για το ποιοι αλγόριθμοι χρησιμοποιούνται για τη σύνδεση σε μια συγκεκριμένη σελίδα, αρκεί να κάνουμε κλικ στο λουκέτο στη μπάρα διευθύνσεων.
Στη συνέχεια, στον Chrome επιλέγουμε τη “Σύνδεση”…
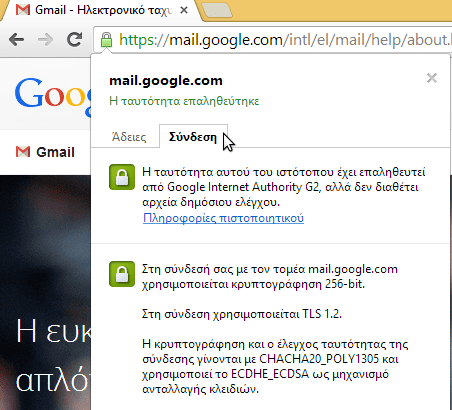
Στον Firefox πηγαίνουμε στο “Περισσότερα για αυτή την ιστοσελίδα”

και βλέπουμε αναλυτικά όλες τις πληροφορίες.
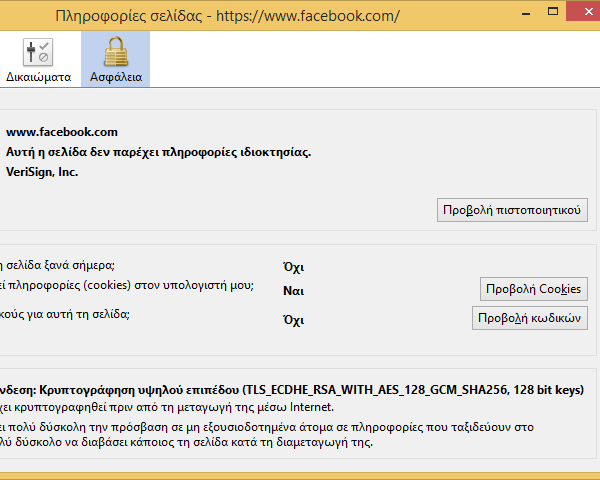
Η σημασία των μαθηματικών στην κρυπτογράφηση δεδομένων
(σημείωση: αν δεν αντέχετε τα μαθηματικά, προσπεράστε ολόκληρη αυτή την ενότητα)
(επίσης, αν οτιδήποτε από τα παρακάτω δεν σας είναι απόλυτα σαφές, γράψτε μας στα σχόλια και θα το διευκρινήσουμε περισσότερο)
Για να ασχοληθεί κάποιος με την επιστήμη της κρυπτογράφησης δεδομένων, η γνώση ανώτερων μαθηματικών είναι πολύ σημαντικότερη από τη γνώση που αφορά τους υπολογιστές και τα δίκτυα.
Αυτό συμβαίνει γιατί συγκεκριμένες μαθηματικές δομές και ιδιότητες των αριθμών, βασισμένες σε θεωρήματα μαθηματικών όπως ο Ευκλείδης, ο Fermat, και ο Euler, είναι που κάνουν τους αλγόριθμους κρυπτογράφησης τόσο δύσκολο να σπάσουν.
Για παράδειγμα, ένας από τους ισχυρότερους και πλέον διαδεδομένους αλγόριθμους για την κρυπτογράφηση δεδομένων στο Internet είναι ο RSA, ένα κρυπτογραφικό σύστημα Public/Asymmetric key με κλειδιά μήκους από 1024 έως 4096 bit.
Η μέθοδος με την οποία ο RSA δημιουργεί το Public και το Private key στηρίζεται στις παρακάτω μαθηματικές έννοιες:
- Τους πρώτους και τους σύνθετους αριθμούς
- Τους ημιπρώτους αριθμούς
- Τον μέγιστο κοινό διαιρέτη
- Τους σχετικά πρώτους αριθμούς
- Την συνάρτηση Euler φ(n)
- Την παραγοντοποίηση πρώτων αριθμών
- Το υπόλοιπο της διαίρεσης και οι ισοϋπόλοιποι αριθμοί
- Τους αντίστροφους αριθμούς και το θεώρημα Euler.
Πριν λοιπόν δούμε πως ακριβώς λειτουργεί ο RSA, ας κάνουμε ένα μικρό φρεσκάρισμα στα μαθηματικά μας.

Οι βασικές μαθηματικές έννοιες
Όπως πιθανώς θυμάστε από το σχολείο:
Πρώτοι και σύνθετοι αριθμοί
Πρώτοι είναι οι αριθμοί που διαιρούνται ακριβώς μόνο με τον εαυτό τους και με τη μονάδα. Οι παρακάτω είναι όλοι οι πρώτοι αριθμοί μέχρι το 100.
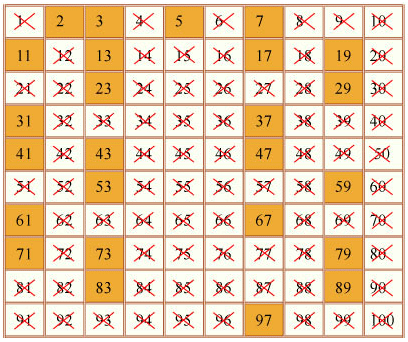
Ο μεγαλύτερος πρώτος αριθμός που έχει ανακαλυφθεί μέχρι στιγμής είναι ο 274,207,281-1, που επιβεβαιώθηκε στις 7 Ιανουαρίου 2016 και ονομάζεται M74207281.
Ο αριθμός αυτός αποτελείται από 22 εκατομμύρια ψηφία, που σημαίνει πως για να τον διαβάσουμε φωναχτά, αν λέμε δύο ψηφία το δευτερόλεπτο, θα μας πάρει πάνω από τέσσερις μήνες για να τον πούμε ολόκληρο.
Οι υπόλοιποι αριθμοί που δεν είναι πρώτοι, ονομάζονται “σύνθετοι αριθμοί”.
Ημιπρώτοι αριθμοί
Ημιπρώτοι ονομάζονται οι αριθμοί που παράγονται από τον πολλαπλασιασμό δύο πρώτων.
15=3*5
8633 = 89*97
Μέγιστος κοινός διαιρέτης
Ο μέγιστος κοινός διαιρέτης δύο αριθμών α και β είναι ο μεγαλύτερος ακέραιος αριθμός που διαιρεί ακριβώς και τους δύο. Συμβολίζεται με ΜΚΔ(a,b)
ΜΚΔ(120,350)=10
ΜΚΔ(150,350)=50
Για να βρούμε το μέγιστο κοινό διαιρέτη μπορούμε να εφαρμόσουμε παραγοντοποίηση (για την οποία θα μιλήσουμε παρακάτω) ή τον Αλγόριθμο του Ευκλείδη.
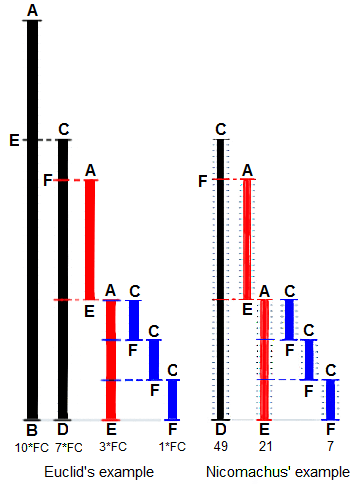
Εξ' ορισμού, ο μέγιστος κοινός διαιρέτης οποιωνδήποτε διαφορετικών πρώτων αριθμών είναι η μονάδα.
ΜΚΔ(89,97)=1
Σχετικά πρώτοι αριθμοί
Οι σχετικά πρώτοι αριθμοί για έναν συγκεκριμένο αριθμό είναι αυτοί που έχουν μέγιστο κοινό διαιρέτη τη μονάδα με τον συγκεκριμένο αριθμό.
Προφανώς όλοι οι πρώτοι αριθμοί είναι και σχετικά πρώτοι μεταξύ τους. Επίσης, σε έναν πρώτο αριθμό x, όλοι ακέραιοι οι αριθμοί από το μηδέν ως το x-1 είναι σχετικά πρώτοι μαζί του.
Μπορούν όμως και αριθμοί που δεν είναι πρώτοι να είναι σχετικά πρώτοι μεταξύ τους. Για παράδειγμα, ο ΜΚΔ(21,22)=1, άρα το 21 και το 22 είναι σχετικά πρώτοι μεταξύ τους.
Η συνάρτηση Euler φ(n)
Ο Leonhard Euler είναι μία από τις μεγαλύτερες μαθηματικές ιδιοφυΐες στην ιστορία…

…και φαίνεται!
Η συνάρτηση Euler για ένα συγκεκριμένο θετικό ακέραιο αριθμό μετράει πόσοι σχετικά πρώτοι αριθμοί υπάρχουν ανάμεσα στο μηδέν και τον συγκεκριμένο αριθμό.
Για παράδειγμα, το 9 έχει μέγιστο κοινό διαιρέτη τη μονάδα με έξι αριθμούς από το 0 ως το 9, τους 1, 2, 4, 5, 7 και 8.
Άρα το φ(9)=6
Εξ ορισμού, το φ(n) για οποιονδήποτε πρώτο αριθμό p είναι φ(n)=(p-1)
Αυτό συμβαίνει γιατί, όπως προαναφέραμε, όλοι οι αριθμοί ανάμεσα στο μηδέν και έναν πρώτο αριθμό είναι σχετικά πρώτοι μαζί του, εκτός από τον ίδιο τον πρώτο αριθμό.
Παραγοντοποίηση Πρώτων
Σύμφωνα με την θεωρία των αριθμών, η παραγοντοποίηση ακεραίων ή παραγοντοποίηση πρώτων αριθμών είναι η ανάλυση ενός σύνθετου αριθμού σε μικρότερους πρώτους αριθμούς, που ονομάζονται παράγοντες.
Πολλαπλασιάζοντας μεταξύ τους αυτούς τους παράγοντες, παίρνουμε τον αρχικό αριθμό.
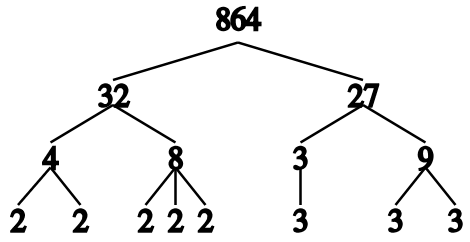
Επίσης, σύμφωνα με τη θεμελιώδη θεωρία αριθμών, κάθε ακέραιος θετικός έχει ένα μοναδικό αποτέλεσμα όσον αφορά την παραγοντοποίηση πρώτων.
Αυτή η ιδιότητα της παραγοντοποίησης είναι πιθανώς ο ισχυρότερος παράγοντας για την ασφάλεια στην κρυπτογράφηση δεδομένων.
Το υπόλοιπο της διαίρεσης και οι ισοϋπόλοιποι αριθμοί
Πριν μάθουμε για δεκαδικούς και κλάσματα, όταν πρωτομαθαίναμε τη διαίρεση πχ 24/10, λέγαμε πως “το 10 χωράει 2 φορές στο 24 και περισσεύουν 4”.
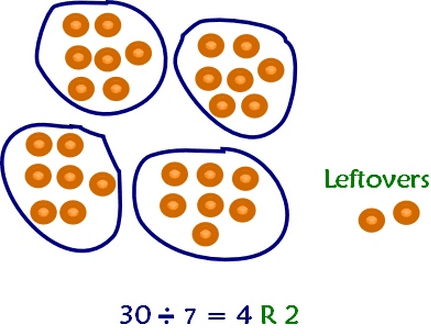
Όσο απίστευτο κι αν φαίνεται, αυτή η λογική είναι ζωτικής σημασίας για την κρυπτογράφηση δεδομένων με τον RSA.
Μαθηματικά, η παραπάνω φράση που αφορά το υπόλοιπο μπορεί να γραφτεί ως:
24 mod 10 = 4
Τώρα, αν δύο αριθμοί έχουν το ίδιο υπόλοιπο στη διαίρεση με τον ίδιο αριθμό, αυτοί οι δύο αριθμοί έχουν μια σχέση συζυγίας (congruence relation) μεταξύ τους.
Η σχέση συζυγίας συμβολίζεται με το ≡, και οι αριθμοί ονομάζονται ισοϋπόλοιποι.
Δηλαδή εφόσον 24 mod 10 = 4 (γιατί περισσεύει 4 στη διαίρεση)
και 54 mod 10 = 4 (καθώς επίσης περισσεύει 4) τότε ισχύει πως
54≡24 mod 10
Η παραπάνω σχέση διαβάζεται “54 ισότιμος του 24 modulo 10”,
ή, εναλλακτικά, “54 ισότιμος του 24 κατά μέτρο 10“.
Αντίστροφοι αριθμοί
Αντίστροφοι είναι δύο αριθμοί που αν τους πολλαπλασιάσουμε μεταξύ τους, μας δίνουν τη μονάδα.
Πχ το x και το x^(-1) (ή αλλιώς το x και το 1/x)
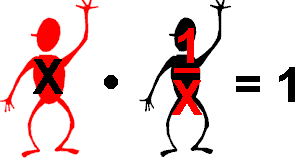
Αυτό που είναι ενδιαφέρον είναι πως αν και μόνο αν δύο αριθμοί α και m είναι σχετικά πρώτοι μεταξύ τους (δηλαδή ΜΚΔ(a,m)=1), τότε ο μικρότερος από τους δύο αριθμούς έχει έναν αριθμό x που είναι αντίστροφος κατά μέτρο του μεγαλύτερου.
Για παράδειγμα, οι αριθμοί 4 και 9 είναι σχετικά πρώτοι μεταξύ τους, γιατί ΜΚΔ(4,9)=1
Αυτό σημαίνει πως υπάρχει ένας ακέραιος αριθμός x<9, για τον οποίο ισχύει
4*X≡1 mod 9
Για να βρεθεί αυτός ο αριθμός, μπορεί να χρησιμοποιηθεί ο διευρυμένος αλγόριθμος του Ευκλείδη.

Στην προκειμένη περίπτωση, ο αριθμός είναι το 7.
4*7=28≡1 mod 9
Πώς χρησιμοποιούνται όλα τα παραπάνω στην κρυπτογράφηση δεδομένων με τον RSA?
Στην πράξη, όταν ο RSA ενεργοποιείται από το TLS, η διαδικασία που ακολουθεί είναι η εξής:
- Παραγωγή δύο πρώτων αριθμών μεγάλου μήκους
Έστω p και q οι αριθμοί αυτοί.
Το ελάχιστο μήκος που μπορεί να έχουν είναι 512 ψηφία. Για να θεωρηθεί ασφαλής η κρυπτογράφηση, θα πρέπει να έχουν μήκος τουλάχιστον 1024 ψηφία.
- Πολλαπλασιασμός των δύο αυτών αριθμών
Με τον πολλαπλασιασμό παράγεται ο ημιπρώτος n
n=p*q
- Εφαρμογή της συνάρτησης Euler στον n
φ(n) = φ(p*q) = φ(p)*φ(q)
Εφόσον ο p και ο q είναι πρώτοι, ισχύει φ(p)=(p-1) και φ(q)=(q-1)
Άρα φ(n)=(p-1)*(q-1), που είναι απείρως πιο εύκολο να υπολογιστεί.
- Παραγωγή του Public key (e)
Το Public Key παράγεται ώστε να είναι ένας πρώτος αριθμός μεταξύ του 3 και του φ(n)
Συμβολίζεται με e και έχει συνήθως την τιμή 65537 (2^16+1).
Αν τύχει το φ(n) να είναι πολλαπλάσιο του 65537, δίνεται άλλη τιμή στο e. Αυτό είναι σχετικά απίθανο να τύχει, αλλά γίνεται έλεγχος.
Eξ' ορισμού ο ΜΚΔ(e, φ(n) )=1
Δεν μας πειράζει το ότι το Public key e είναι γνωστό και δεν είναι τυχαίος αριθμός. Έτσι κι αλλιώς είναι διαθέσιμο σε όλους. Το σημαντικό είναι να μην μπορεί να προκύψει το Private key από το Public key
- Παραγωγή Private key
Από τη στιγμή που το Public key έχει μέγιστο κοινό διαιρέτη τη μονάδα με το φ(n), με τον εκτεταμένο αλγόριθμο του Ευκλείδη μπορούμε να βρούμε γρήγορα τον αντίστροφό του κατά μέτρο φ(n).
Δηλαδή έναν αριθμό d έτσι ώστε
e*d≡1 mod φ(n)
Αυτός ο αριθμός d είναι το private key.
- Κρυπτογράφηση δεδομένων και αποκρυπτογράφηση
Πλέον, με τα κλειδιά έτοιμα, ο RSA είναι έτοιμος να κρυπτογραφήσει τα δεδομένα.
Ουσιαστικά, όλο το κείμενο προς κρυπτογράφηση, μέσα από μια διαδικασία που δεν θα περιγράψουμε αυτή τη στιγμή, παίρνει μία αριθμητική τιμή, έστω m.
Ο RSA μετασχηματίζει αυτή την τιμή m μέσα από την παρακάτω συνάρτηση με βάση το κλειδί k, με n το γινόμενο των πρώτων αριθμών:
F(m,k)=m^k mod n
Για τη συνάρτηση αυτή, υπάρχουν δύο περιπτώσεις:
Κατά την κρυπτογράφηση δεδομένων, ο RSA εφαρμόζει τη συνάρτηση ως εξής:
F(m,e)=m^e mod n = c, όπου m είναι το μήνυμα, e είναι το public key και c είναι το κρυπτογραφημένο μήνυμα.
Στην αποκρυπτογράφηση δεδομένων, η συνάρτηση είναι
F(c,d)=c^d mod n = m, όπου c είναι τα κρυπτογραφημένα δεδομένα, d είναι το private key και m είναι το αποκρυπτογραφημένο κείμενο.
Επίσης, ο RSA λειτουργεί και αντιστρόφως, μπορεί να κάνει κρυπτογράφηση δεδομένων με το private key και να τα αποκρυπτογραφήσει με το Public, με τις ίδιες εξισώσεις.
Έτσι λοιπόν λειτουργεί ο RSA.
Αριθμητικό παράδειγμα για το πώς λειτουργεί ο RSA
Για όσους δεν είμαστε μαθηματικοί, ένα πρακτικό παράδειγμα δείχνει πιο καθαρά πως λειτουργεί ο RSA κατά την κρυπτογράφηση δεδομένων.
- Παραγωγή δύο πρώτων αριθμών
Επειδή θα μας πάρει περίπου 2 χρόνια να κάνουμε πράξεις με αριθμούς των 1024 ψηφίων με το χέρι, έστω πως οι πρώτοι αριθμοί που παράγουμε στον χειροκίνητο RSA μας είναι p=11 και q=13.
- Πολλαπλασιασμός των δύο αυτών αριθμών
n=11*13=143
- Εφαρμογή της συνάρτησης Euler στον n
Άρα φ(n)=(p-1)*(q-1)=10*12=120
- Παραγωγή του Public key (e)
Χρειαζόμαστε έναν πρώτο αριθμό από το 3 ως το φ(n)120, που να έχει μέγιστο κοινό διαιρέτη 1 με το 120.
Ας επιλέξουμε το e=7.
ΜΚΔ(7, 120)=1
- Παραγωγή Private key (d)
Θέλουμε έναν αριθμό d έτσι ώστε
e*d≡1 mod φ(n) δηλαδή 7*d≡1 mod 120.
Με τον εκτεταμένο αλγόριθμο του Ευκλείδη βρίσκουμε τον αριθμό d=103.
Για επαλήθευση έχουμε e*d≡1 mod φ(n), δηλαδή 7*103=721≡1 mod 120, που ισχύει.
- Κρυπτογράφηση δεδομένων και αποκρυπτογράφηση
Ας πούμε πως τα δεδομένα μας είχαν την τιμή m=9.
Για την κρυπτογράφηση δεδομένων έχουμε m^e mod n= 9^7 mod 143 = 48
Άρα, το αρχικό κείμενο m=9 με την κρυπτογράφηση έγινε c=48.
Για την αποκρυπτογράφηση έχουμε: c^d mod n = 48^103 mod 143 = 9
Και έχουμε ξανά το m=9.

Παρατηρήστε πως τέτοιες πράξεις, όπως το 48^103 (που θα ήταν ασύγκριτα μεγαλύτερες με πραγματικά νούμερα) είναι που κάνουν τον RSA τόσο απαιτητικό σε υπολογισμούς, και χρησιμοποιείται η υβριδική μέθοδος με το symmetric key.
Αλλιώς, ένας server που έχει να εξυπηρετήσει εκατομμύρια επισκέπτες την ημέρα, θα ήταν αδύνατον να ανταπεξέλθει στην απαιτούμενη επεξεργαστική ισχύ.

Γιατί η κρυπτογράφηση δεδομένων με τον RSA είναι απόλυτα ασφαλής
Ας πούμε πως θέλαμε να σπάσουμε τον κώδικα του παραδείγματος του RSA που φτιάξαμε παραπάνω.
Σαν εξωτερικοί παρατηρητές, οι μόνες τιμές που βλέπουμε είναι το Public key, που είναι 7, το n που είναι 143 και το κρυπτογραφημένο κείμενο c=48.
Δεν βλέπουμε όμως πουθενά τους πρώτους αριθμούς που χρησιμοποιήθηκαν για να φτιάξουν το n, με τους οποίους θα μπορούσαμε να υπολογίσουμε εύκολα το φ(n). Και χωρίς το φ(n) είναι αδύνατον να υπολογίσουμε το private key d.
Από τη στιγμή που ο n είναι 143 στο παράδειγμα, θα μπορούσαμε να τον παραγοντοποιήσουμε και με το χέρι, και πρακτικά να σπάσουμε τον κωδικό.

Αν όμως ο n είναι ένας αριθμός με 309 ψηφία, όπως ισχύει στον RSA-1024, δεν έχει υπάρξει υπολογιστής που να μπορέσει να εφαρμόσει επιτυχώς παραγοντοποίηση πρώτων σε αυτόν.
Ο μεγαλύτερος ημιπρώτος αριθμός που έχουμε καταφέρει να παραγοντοποιήσουμε είναι ο RSA-768, ένας αριθμός 232 ψηφίων:
RSA-768 = 1230186684530117755130494958384962720772853569595334792197322452151726400507263657518745202199786469389956474942774063845925192557326303453731548268507917026122142913461670429214311602221240479274737794080665351419597459856902143413
Η παραγοντοποίησή του ήταν:
RSA-768 = 33478071698956898786044169848212690817704794983713768568912431388982883793878002287614711652531743087737814467999489 × 36746043666799590428244633799627952632279158164343087642676032283815739666511279233373417143396810270092798736308917
Για να βρεθεί το παραπάνω αποτέλεσμα, χρειάστηκαν πολλαπλοί ερευνητές και εκατοντάδες υπολογιστές να εργάζονται για 2 χρόνια.
Αν ένας μονοπύρηνος AMD Opteron 2,2GHz επιχειρούσε να κάνει όλες αυτές τις πράξεις, θα χρειαζόταν κυριολεκτικά 2.000 χρόνια.
Το διαβόητο ransomware cryptolocker χρησιμοποιεί κρυπτογράφηση δεδομένων RSA-2048 – γι' αυτό και όποιος το κόλλησε, η μόνη λύση ήταν να πληρώσει, αν ήθελε πίσω τα δεδομένα του.
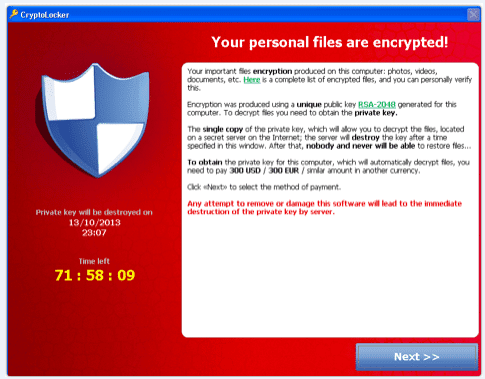
Χρειάστηκαν οι εντατικές προσπάθειες από τρεις διαφορετικές εταιρείες ασφαλείας για να εντοπίσουν το ιδιωτικό κλειδί που τελικά επέτρεψε την αποκρυπτογράφηση δωρεάν.
Η σημασία των τυχαίων αριθμών στην κρυπτογράφηση δεδομένων
Στην κρυπτογράφηση δεδομένων RSA είναι εξαιρετικά σημαντικό οι πρώτοι αριθμοί που θα παραχθούν να είναι πραγματικά τυχαίοι.
Το ίδιο ισχύει και για τα κλειδιά σε αλγόριθμους symmetric key, όπως ο AES-128, και σε όλους πρακτικά τους αλγορίθμους κρυπτογράφησης.
Γιατί όμως είναι τόσο μεγάλο ζήτημα η τυχαιότητα?
Υπολογιστές, ντετερμινισμός, και η δυσκολία του τυχαίου
Ο υπολογιστής είναι ένα ντετερμινιστικό σύστημα. Αυτό σημαίνει πως αν του κάνουμε την ίδια ερώτηση, όσες φορές κι αν του την κάνουμε, θα έχει πάντοτε την ίδια απάντηση.
Αυτό είναι πρακτικό για την καθημερινή χρήση του υπολογιστή – κανείς δεν θα ήθελε να έκανε διπλό κλικ στο word και να άνοιγε στη θέση του ένα τυχαίο, άσχετο πρόγραμμα.
Οι υπολογιστές είναι προγραμματισμένοι έτσι ώστε να μην είναι τίποτα τυχαίο, ώστε να ακολουθούν πάντα τις οδηγίες, τους αλγόριθμους των προγραμμάτων.
Όσον αφορά την κρυπτογραφία, όμως, αυτή η μέθοδος λειτουργίας είναι καταστροφική.
Το πρόβλημα είναι πως ο υπολογιστής δεν μπορεί να παράγει τίποτα από το μηδέν.
Μπορεί να πάρει έναν αριθμό και να τον μετασχηματίσει. Να τον περάσει από έναν μακρύ και περίπλοκο αλγόριθμο, έτσι ώστε στο τέλος να είναι ένας εντελώς διαφορετικός αριθμός.
Το θέμα όμως είναι πως ο ίδιος αρχικός αριθμός θα δίνει πάντοτε το ίδιο τελικό αποτέλεσμα. Ο αλγόριθμος είναι ένας, δεν αλλάζει, όσο περίπλοκος κι αν είναι. Οι αριθμοί που παράγονται, λοιπόν, δεν είναι πραγματικά τυχαίοι. Είναι ψευδοτυχαίοι (pseudo-random).
Ο μόνος τρόπος να επιτευχθεί πραγματική τυχαιότητα είναι ο αρχικός αριθμός που θα δοθεί στον υπολογιστή για να μετασχηματίσει, να είναι εκείνος πραγματικά τυχαίος.

Κάποια προγράμματα, όπως το Truecrypt χρησιμοποιούν δεδομένα από την κίνηση του ποντικιού από τον χρήστη.
Το HotBits, τμήμα του Ελβετικού site Fournilab, χρησιμοποιεί τη ραδιενεργό διάσπαση ενός ραδιενεργού υλικού, που είναι απρόβλεπτο το πότε θα συμβεί.

Στο Random.org – το οποίο χρησιμοποιούμε και στο PCsteps για να βρούμε τους τυχαίους νικητές του εκάστοτε διαγωνισμού – μετρούν τον ατμοσφαιρικό θόρυβο, χρησιμοποιώντας τα παράσιτα ενός ραδιοφώνου.
Στο Lavarand, όσο λειτουργούσε, χρησιμοποιούσαν lava lamps.

Γενικά, πάντως, η παραγωγή τυχαίων αριθμών στους υπολογιστές είναι κάτι που χρειάζεται σοβαρή μελέτη από τον σχεδιαστή ενός συστήματος.
Γιατί είναι τόσο απαραίτητη η τυχαιότητα στην κρυπτογραφία
Αναφέραμε πως ο αλγόριθμος AES παράγει ένα τυχαίο κλειδί 128 bit, που μπορεί να έχει πάνω από 300.000.000.000.000.000.000.000.000.000.000.000 πιθανούς συνδυασμούς.
Αν όμως τα δεδομένα τα οποία επεξεργάζεται ο αλγόριθμος για να δημιουργήσει το κάθε κλειδί δεν είναι πραγματικά τυχαία, τότε ούτε και τα τελικά κλειδιά θα είναι τυχαία. Οι πιθανοί συνδυασμοί μπορεί να είναι σημαντικά λιγότεροι, μειώνοντας την ασφάλεια ολόκληρου του συστήματος.

Ακόμα χειρότερα, αν τα δεδομένα δεν είναι πραγματικά τυχαία, μπορεί κάποιος να αναλύσει έναν αλγόριθμο στο βαθμό που να καταλάβει τη λειτουργία του, και έτσι να μπορεί να προβλέψει ποιο θα είναι το επόμενο αποτέλεσμα που θα δώσει.
Γιατί υπάρχουν ακόμα hacker?
Θεμελιώσαμε πως τα σύγχρονα πρωτόκολλα για την κρυπτογράφηση δεδομένων είναι αδύνατον να σπάσουν.
Άρα, λοιπόν, γιατί δεν είναι όλα τα συστήματα απαραβίαστα? Γιατί ακόμα και δίκτυα όπως του Πενταγώνου, της Apple, του Twitter, και των New York Times πέφτουν θύματα hacker?
Δείτε το άρθρο μας σχετικά με το Spear Phishing, την πιο επικίνδυνη επίθεση που μπορεί να παραβιάσει ακόμα και το πιο ασφαλές σύστημα στον κόσμο, γιατί χτυπάει στον πιο αδύναμο κρίκο: τον άνθρωπο.
Δείτε και το σχετικό comic strip του XKCD.

Γενικά, υπάρχουν ασύγκριτα πιο εύκολοι τρόποι για τους hacker ώστε να αποκτήσουν τις πληροφορίες που θέλουν από το να προσπαθήσουν να σπάσουν την κρυπτογράφηση δεδομένων.
Είναι λοιπόν ζωτικής σημασίας να ακολουθούμε τις αρχές της ηλεκτρονικής ασφάλειας. Γιατί οι καλύτεροι αλγόριθμοι κρυπτογράφησης στον κόσμο δεν θα μας βοηθήσουν σε τίποτα αν κολλήσουμε έναν keylogger που διαβάζει όλα όσα γράφουμε στο πληκτρολόγιο.
Έχετε απορίες σχετικά με την κρυπτογράφηση δεδομένων?
Η κρυπτογράφηση δεδομένων είναι ένα θέμα που οι ειδικοί σπουδάζουν χρόνια για να κατανοήσουν, και μια απλή δημοσίευση 4.900 λέξεων δεν κάνει ειδικούς ούτε εμάς, ούτε και εσάς.
Ελπίζουμε πάντως να ανοίξαμε ένα έστω μικρό παράθυρο στο πως λειτουργούν τα συστήματα που κρατούν ασφαλείς τις πληροφορίες μας, και μας επιτρέπουν να επικοινωνήσουμε ιδιωτικά, να κάνουμε αγορές μέσω Internet, και ασφαλείς συναλλαγές στο ebanking.
Αν έχετε περισσότερες απορίες για την κρυπτογράφηση δεδομένων, γράψτε μας στα σχόλια.